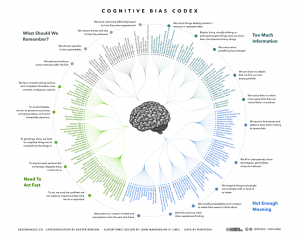
How Many Cognitive Biases Are There?
In my critical thinking class, we begin by studying 17 cognitive biases that are drawn from Peter Facione’s excellent textbook, Think Critically. (I’ve also summarized these here, here, here, and here). I like the way Facione organizes and describes the major biases. His work is very teachable. And 17 is a manageable number of biases to teach and discuss.
While the 17 biases provide a good introduction to the topic, there are more biases that we need to be aware of. For instance, there’s the survivorship bias. Then there’s swimmer’s body fallacy. And the Ikea effect. And the self-herding bias. And don’t forget the fallacy fallacy. How many biases are there in total? Well, it depends on who’s counting and how many hairs we’d like to split. One author says there are 25. Another suggests that there are 53. Whatever the precise number, there are enough cognitive biases that leading consulting firms like McKinsey now have “debiasing” practices to help their clients make better decisions.
The ultimate list of cognitive biases probably comes from Wikipedia, which identifies 104 biases. (Click here and here). Frankly, I think Wikipedia is splitting hairs. But I do like the way Wikipedia organizes the various biases into four major categories. The categorization helps us think about how biases arise and, therefore, how we might overcome them. The four categories are:
1) Biases that arise from too much information – examples include: We notice things already primed in memory. We notice (and remember) vivid or bizarre events. We notice (and attend to) details that confirm our beliefs.
2) Not enough meaning – examples include: We fill in blanks from stereotypes and prior experience. We conclude that things that we’re familiar with are better in some regard than things we’re not familiar with. We calculate risk based on what we remember (and we remember vivid or bizarre events).
3) How we remember – examples include: We reduce events (and memories of events) to the key elements. We edit memories after the fact. We conflate memories that happened at similar times even though in different places or that happened in the same place even though at different times, … or with the same people, etc.
4) The need to act fast – examples include: We favor simple options with more complete information over more complex options with less complete information. Inertia – if we’ve started something, we continue to pursue it rather than changing to a different option.
It’s hard to keep 17 things in mind, much less 104. But we can keep four things in mind. I find that these four categories are useful because, as I make decisions, I can ask myself simple questions, like: “Hmmm, am I suffering from too much information or not enough meaning?” I can remember these categories and carry them with me. The result is often a better decision.
Surviving The Survivorship Bias

You too can be popular.
Here are three articles from respected sources that describe the common traits of innovative companies:
The 10 Things Innovative Companies Do To Stay On Top (Business Insider)
The World’s 10 Most Innovative Companies And How They Do It (Forbes)
Five Ways To Make Your Company More Innovative (Harvard Business School)
The purpose of these articles – as Forbes puts it – is to answer a simple question: “…what makes the difference for successful innovators?” It’s an interesting question and one that I would dearly love to answer clearly.
The implication is that, if your company studies these innovative companies and implements similar practices, well, then … your company will be innovative, too. It’s a nice idea. It’s also completely erroneous.
How do we know the reasoning is erroneous? Because it suffers from the survivorship fallacy. (For a primer on survivorship, click here and here). The companies in these articles are picked because they are viewed as the most innovative or most successful or most progressive or most something. They “survive” the selection process. We study them and abstract out their common practices. We assume that these common practices cause them to be more innovative or successful or whatever.
The fallacy comes from an unbalanced sample. We only study the companies that survive the selection process. There may well be dozens of other companies that use similar practices but don’t get similar results. They do the same things as the innovative companies but they don’t become innovators. Since we only study survivors, we have no basis for comparison. We can’t demonstrate cause and effect. We can’t say how much the common practices actually contribute to innovation. It may be nothing. We just don’t know.
Some years ago, I found a book called How To Be Popular at a used-book store. Written for teenagers, it tells you what the popular kids do. If you do the same things, you too can be popular. It’s cute and fluffy and meaningless. In fact, to someone beyond adolescence, it’s obvious that it’s meaningless. Doing what the popular kids do doesn’t necessarily make your popular. We all know that.
I bought the book as a keepsake and a reminder that the survivorship fallacy can pop up at any moment. It’s obvious when it appears in a fluffy book written for teens. It’s less obvious when it appears in a prestigious business journal. But it’s still a fallacy.
Now You See It, But You Don’t
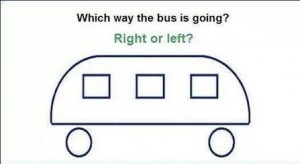
What don’t you see?
The problem with seeing is that you only see what you see. We may see something and try to make reasonable deductions from it. We assume that what we see is all there is. All too often, the assumption is completely erroneous. We wind up making decisions based on partial evidence. Our conclusions are wrong and, very often, consistently biased. We make the same mistake in the same way consistently over time.
As Daniel Kahneman has taught us: what you see isn’t all there is. We’ve seen one of his examples in the story of Steve. Kahneman present this description:
Steve is very shy and withdrawn, invariably helpful but with little interest in people or in the world of reality. A meek and tidy soul, he has a need for order and structure, and a passion for detail.
Kahneman then asks if it’s more likely that Steve is a farmer or a librarian?
If you read only what’s presented to you, you’ll most likely guess wrong. Kahneman wrote the description to fit our stereotype of a male librarian. But male farmers outnumber male librarians by a ratio of about 20:1. Statistically, it’s much more likely that Steve is a farmer. If you knew the base rate, you would guess Steve is a farmer.
We saw a similar example with World War II bombers. Allied bombers returned to base bearing any number of bullet holes. To determine where to place protective armor, analysts mapped out the bullet holes. The key question: which sections of the bomber were most likely to be struck? Those are probably good places to put the armor.
But the analysts only saw planes that survived. They didn’t see the planes that didn’t make it home. If they made their decision based only on the planes they saw, they would place the armor in spots where non-lethal hits occurred. Fortunately, they realized that certain spots were under-represented in their bullet hole inventory – spots around the engines. Bombers that were hit in the engines often didn’t make it home and, thus, weren’t available to see. By understanding what they didn’t see, analysts made the right choices.
I like both of these examples but they’re somewhat abstract and removed from our day-to-day experience. So, how about a quick test of our abilities? In the illustration above, which way is the bus going?
Study the image for a while. I’ll post the answer soon.
Survivorship Bias

Protect the engines.
Are humans fundamentally biased in our thinking? Sure, we are. In fact, I’ve written about the 17 biases that consistently crop up in our thinking. (See here, here, here, and here). We’re biased because we follow rules of thumb (known as heuristics) that are right most of the time. But when they’re wrong, they’re wrong in consistent ways. It helps to be aware of our biases so we can correct for them.
I thought my list of 17 provided a complete accounting of our biases. But I was wrong. In fact, I was biased. I wanted a complete list so I jumped to the conclusion that my list was complete. I made a subtle mistake and assumed that I didn’t need to search any further. But, in fact, I should have continued my search.
The latest example I’ve discovered is called the survivorship bias. Though it’s new to me, it’s old hat to mathematicians. In fact, the example I’ll use is drawn from a nifty new book, How Not to Be Wrong: The Power of Mathematical Thinking by Jordan Ellenberg.
Ellenberg describes the problem of protecting military aircraft during World War II. If you add too much armor to a plane, it becomes a heavy, slow target. If you don’t add enough armor, even a minor scrape can destroy it. So what’s the right balance?
American military officers gathered data from aircraft as they returned from their missions. They wanted to know where the bullet holes were. They reasoned that they should place more armor in those areas where bullets were most likely to strike.
The officers measured bullet holes per square foot. Here’s what they found:
Engine 1.11 bullet holes per square foot
Fuel System 1.55
Fuselage 1.73
Rest of plane 1.8
Based on these data, it seems obvious that the fuselage is the weak point that needs to be reinforced. Fortunately, they took the data to the Statistical Research Group, a stellar collection of mathematicians organized in Manhattan specifically to study problems like these.
The SRG’s recommendation was simple: put more armor on the engines. Their recommendation was counter-intuitive to say the least. But here’s the general thrust of how they got there:
- In the confusion of air combat, bullets should strike almost randomly. Bullet holes should be more-or-less evenly distributed. The data show that the bullet holes are not evenly distributed. This is suspicious.
- The data were collected from aircraft that returned from their missions – the survivors. What if we included the non-survivors as well?
- There are fewer bullet holes on engines than one would expect. There are two possible explanations: 1) Bullets don’t strike engines for some unexplained reason, or; 2) Bullets that strike engines tend to destroy the airplane – they don’t return and are not included in the sample.
Clearly, the second explanation is more plausible. Conclusion: the engine is the weak point and needs more protection. The Army followed this recommendation and probably saved thousands of airmen’s lives.
It’s a colorful example but may seem distant form our everyday experiences. So, here’s another example from Ellenberg’s book. Let’s say we want to study the ten-year performance of a class of mutual funds. So, we select data from all the mutual funds in the category from 2004 as the starting point. Then we collect similar data from 2014 as the end point. We calculate the percentage growth and reach some conclusions. Perhaps we conclude that this is a good investment category.
What’s the error in our logic? We’ve left out the non-survivors – funds that existed in 2004 but shut down before 2014. If we include them, overall performance scores may decline significantly. Perhaps it’s not such a good investment after all.
What’s the lesson here? Don’t jump to conclusions. If you want to survive, remember to include the non-survivors.